数式内の「--」とは何か?
数式の中に「--」と、マイナス記号を2つ続ける書き方を見たことはありませんか?あまり良い例ではありませんけど、たとえばこんな感じ。
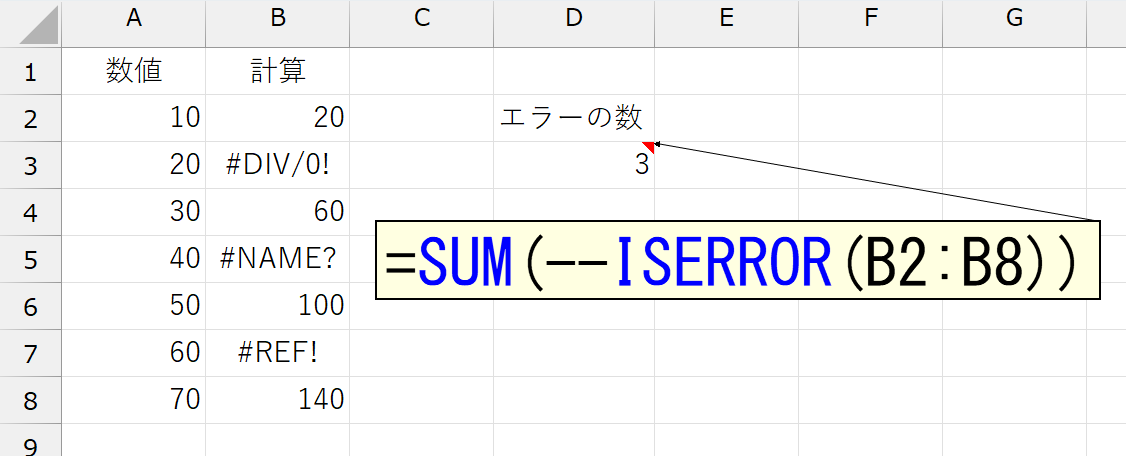
この「--」とは何か?どういう意味で、どんな働きをしているのかを解説します。
TRUEとFALSE
まずは、TRUEとFALSEについて理解してください。TRUEとは"正しい"ということで、FALSEは"正しくない"です。両者をまとめて「論理値」と呼び、TRUEでないものはFALSEであり、FALSEでないものはTRUEという関係です。要するに、何かのスイッチが"オン"か"オフ"か、みたいなイメージです。論理値の定義について深掘りすると、すごく"ややこしい"話になりますので、ここでは割愛します。本稿では、論理値であるTRUEとFALSEを計算する場面だけを考えてみます。
下図をご覧ください。
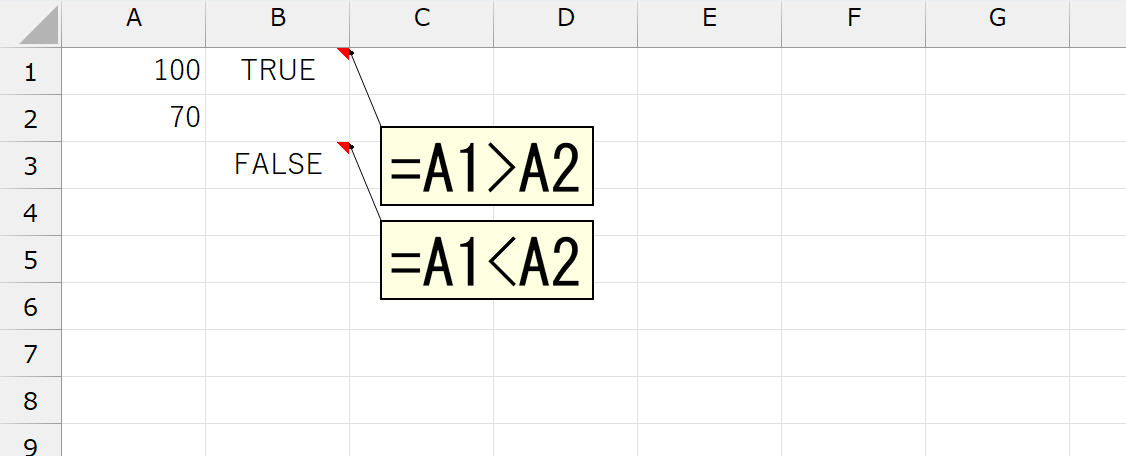
セルA1に数値の「100」を入力し、セルA2には「70」を入力しています。セルB1には「=A1>A2」という数式を入力しました。「セルA1はセルA2より大きい」という意味です。もちろん、これは"正しい"です。そこで、数式は"正しい"を表す"TRUE"を返しました。同じように、セルB3の「=A1<A2」は「セルA1はセルA2より小さい」ですから"正しくない"の"FALSE"になりました。さて、この"TRUE"と"FALSE"を計算に使ってみます。まずは、それぞれ「1」を足してみましょう。
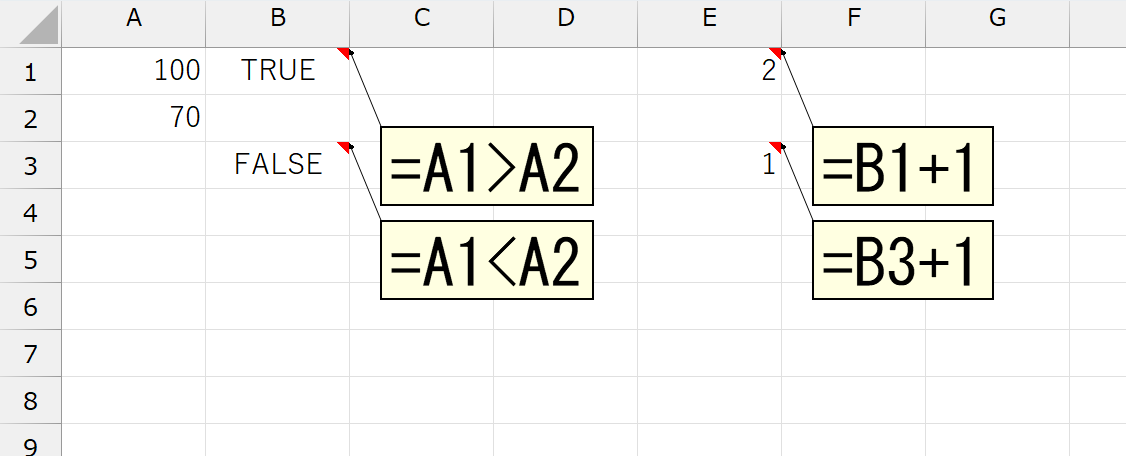
結果から推測するに、どうやら"TRUE"は「1」で、"FALSE"は「0」として計算されているようです。念のため、違う計算もしてみます。
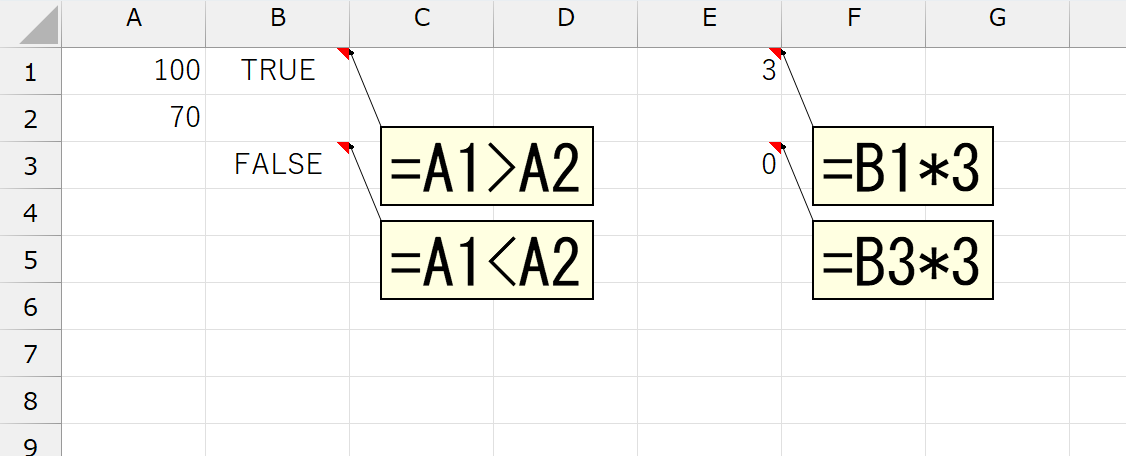
間違いありません。このように、論理値を計算するとき、"TRUE"は「1」で、"FALSE"は「0」として扱われます。これ、すごく重要な基礎ですので、忘れないようにしてくださいね。
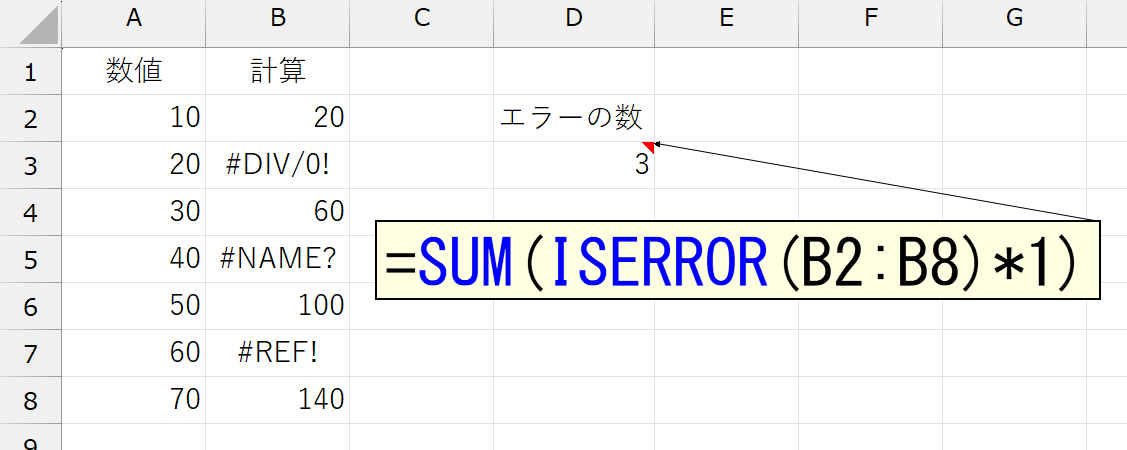
エラーの数式は何個ある?
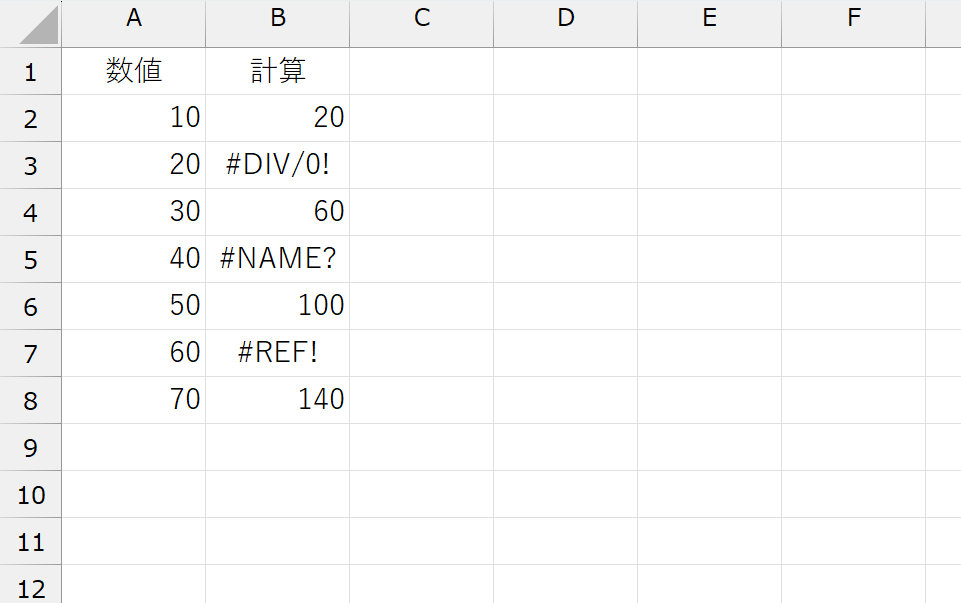
上図のA列には適当な数値が入っています。特に意味はありません。隣のB列に何らかの数式を入力して、何らかの計算をしたとします。その結果、B列に入力した数式のうち、いくつかがエラーになりました。どんな数式を入力したのか、なぜエラーになったのかの原因などは、まったく関係ありません。考えないでください。とにかく、B列に入力した数式のうち「エラーになっている数式は何個あるか」をカウントしたいんです。
Excelには、あるセルがエラーかどうかを判定する関数が用意されています。それがISERROR関数です。ISERROR関数は、引数に指定したセル(というか数式)がエラーだったとき"TRUE"を返し、エラーでなかったときは"FALSE"を返します。
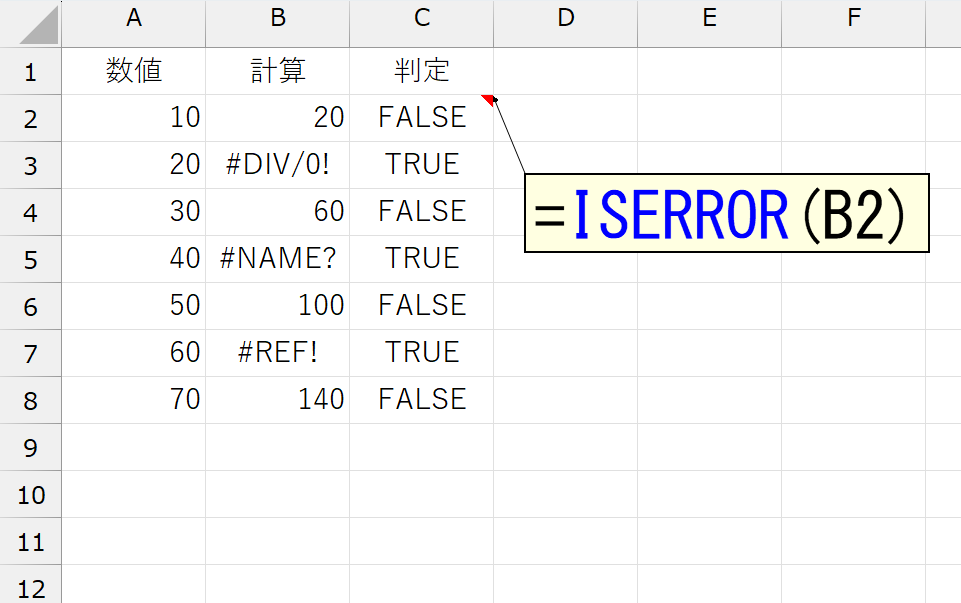
セルC2に「=ISERROR(B2)」という数式を入力して、セルC8までコピーした結果が上図です。正しく判定されていますね。ここで思い出していただきたいのは、論理値を計算するとき、"TRUE"は「1」で、"FALSE"は「0」として扱われるということ。だったら、C列の結果をSUM関数で合計してやれば、3つの"TRUE"がそれぞれ「1」として扱われ、それ以外の"FALSE"はすべて「0」なのですから、結果は「3」になるはずです。
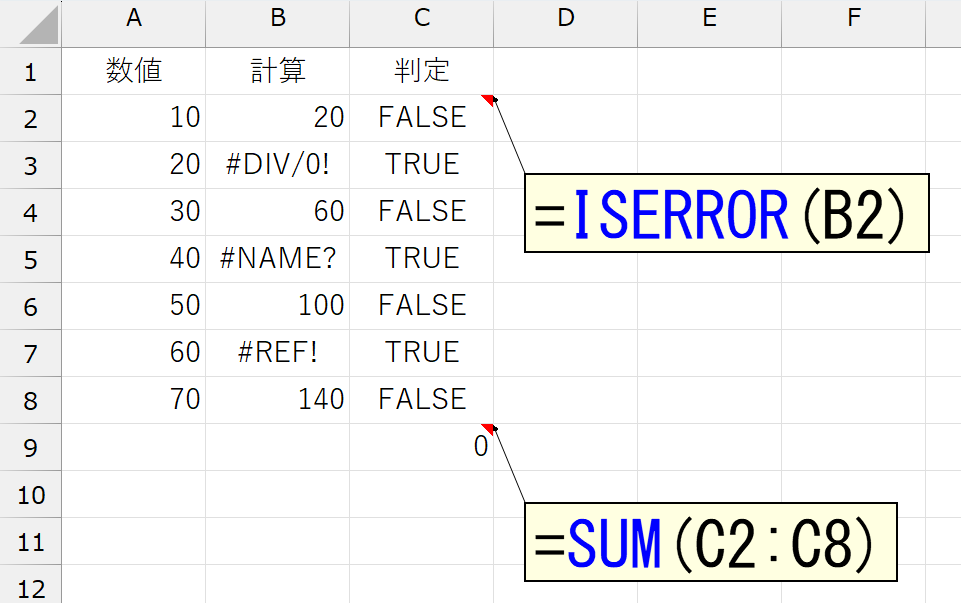
ありゃ?なぜか、うまくいきません。しょんぼりへにょんです。これ、考え方は正しいはずなのに、なぜ計算されないのでしょう?その原因は、SUM関数の仕様です。SUM関数のヘルプには、次のように記載されています。

SUM関数の、この仕様をご存じない方は多いです。つまり今回失敗したのは「論理値を計算しようとした」ことではなく、その計算に「SUM関数を使った」ことが原因です。その証拠に、"TRUE"と"FALSE"のセルを1つずつ足せば、正しく計算されます。
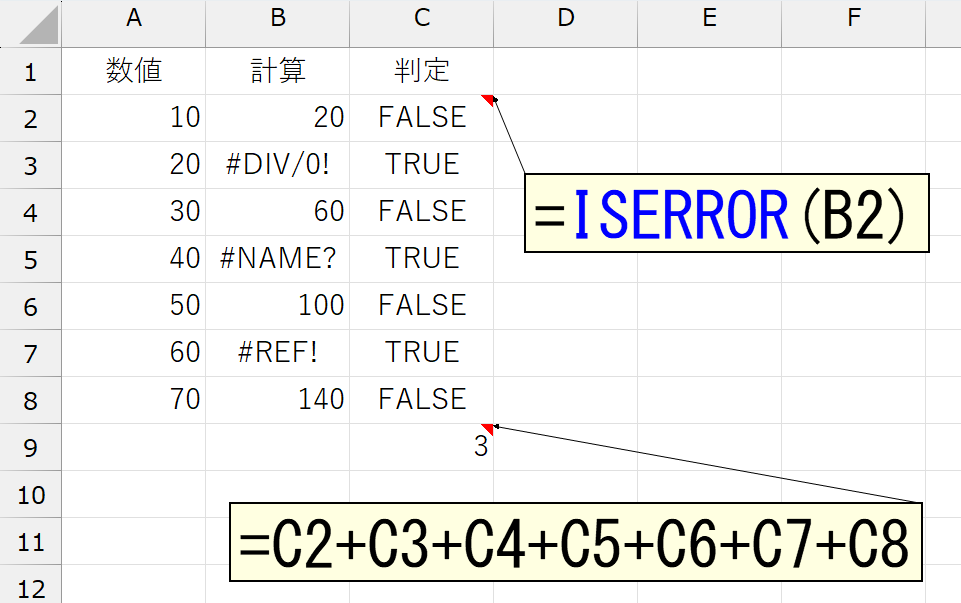
ここ、勘違いしやすいので注意が必要です。テストに出ますよ。
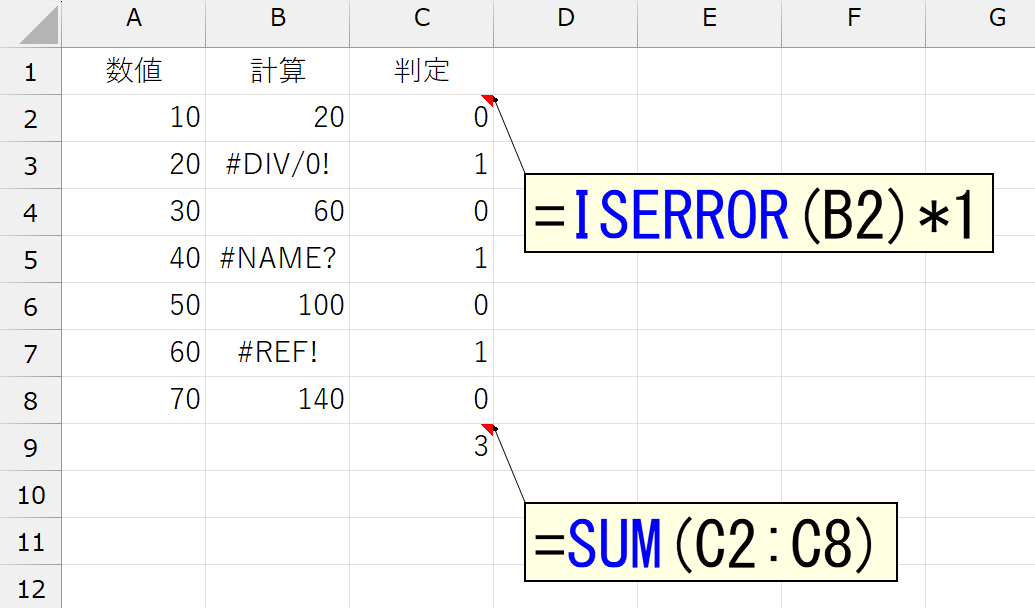
SUM関数で合計したいのであれば、"TRUE"と"FALSE"を何らかの方法で「1」と「0」に変換できればOKです。なら、話は簡単です。ISERROR関数が返す結果を計算してやればいいんです。とはいえ、まったく変な計算結果になっても困ります。計算は計算でも「計算した結果が変わらない」ような計算をしてやります。たとえば、「1」を掛け算するとか。
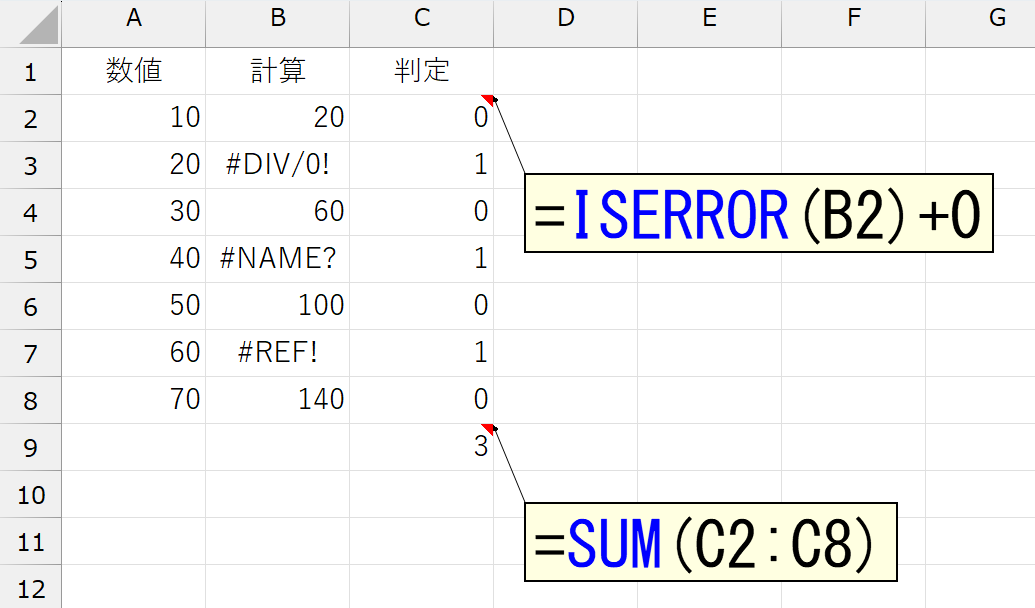
あるいは、「0」を足してもいいですね。どちらでも同じです。
1つの数式にまとめる
ここまでの流れは理解できましたか?では、今回使ったSUM関数とISERROR関数を、1つの数式にまとめてみましょう。
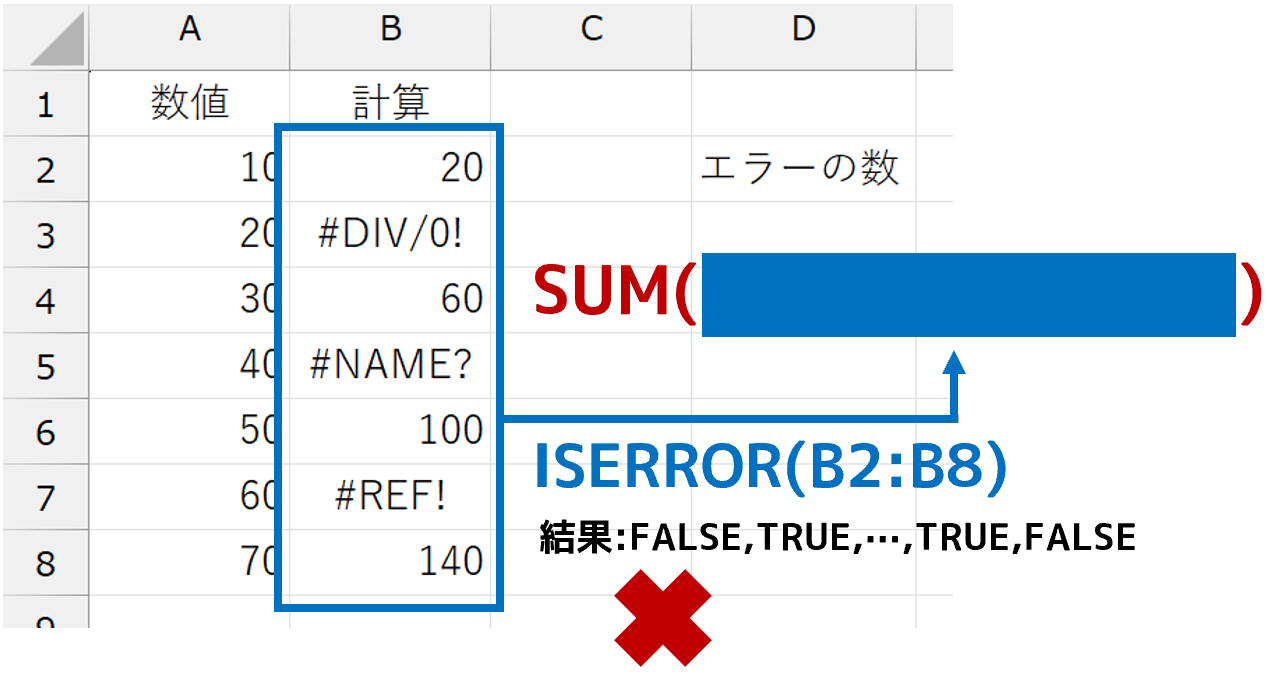
最終的に合計を求めるのですから、数式の大外(左端)にはSUM関数がきます。SUM関数の引数には、セル範囲B2:B8が「エラーかどうか」を判定するISERROR関数を指定します。しかし、ISERROR関数は論理値("TRUE"または"FALSE")を返します。このままでは、SUM関数で合計できません。
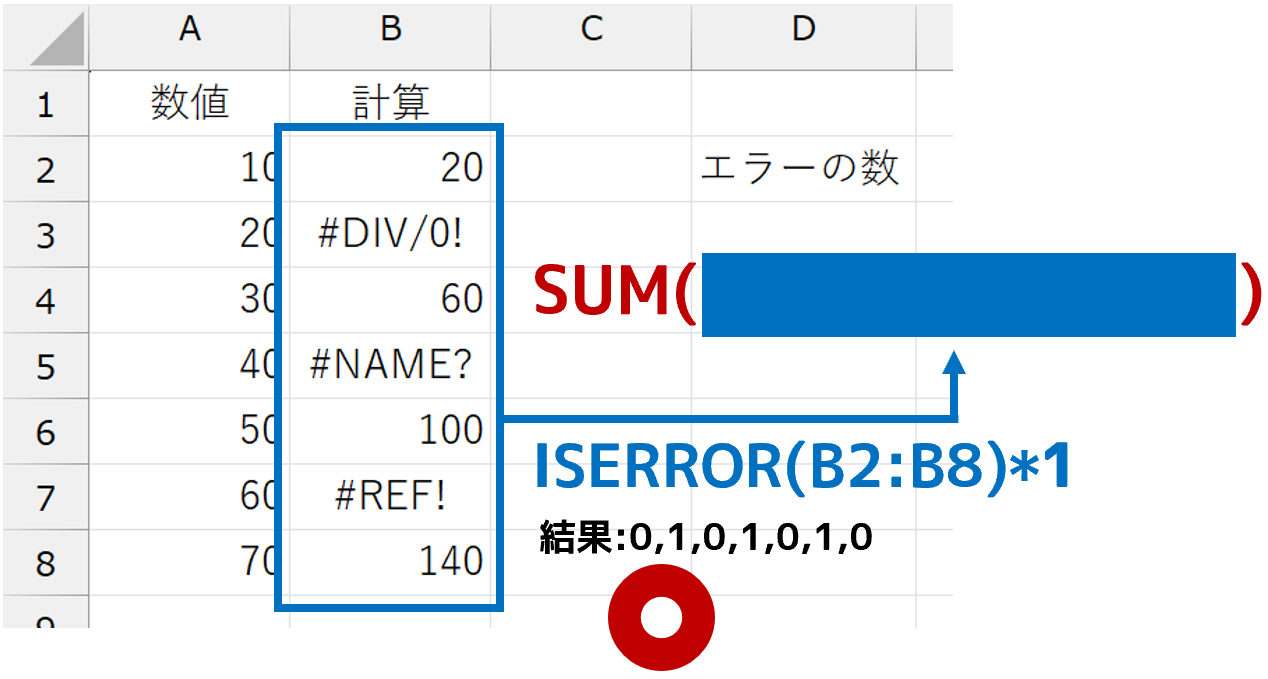
これで完成です。
計算結果を変えない計算
ここまでの話で、ポイントとなるのは「計算しても結果を変えない」ような計算を施したところです。"TRUE"と"FALSE"は論理値ですが、計算で使うときには「1」や「0」といった整数として扱われます。上記のように、任意の整数に対して、1を掛け算(乗法)したり、0を足し算(加法)しても、元の整数は変わりません。余談ですが、この「1」を乗法単位元、「0」を加法単位元などと呼びます。
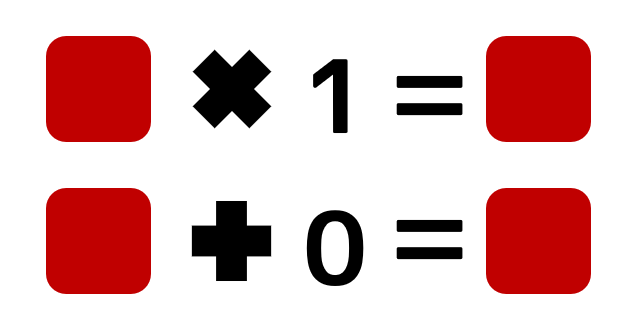
さて、話は変わります。次は「正の整数にマイナス(-)をつけたら」どうなるかを考えてみましょう。ここでは、正の整数として数値の「3」を例にします。「3」にマイナス(-)をつけたら「-3」です。「3」が「-3」になったということは、これ「3に-1を掛け算した」のと同じですよね。つまり「-3」というのは「3×(-1)」の計算をしたようなものと考えられます。余談ですが、このときの「-3」を「3の反数」とか"逆元"などといいます。
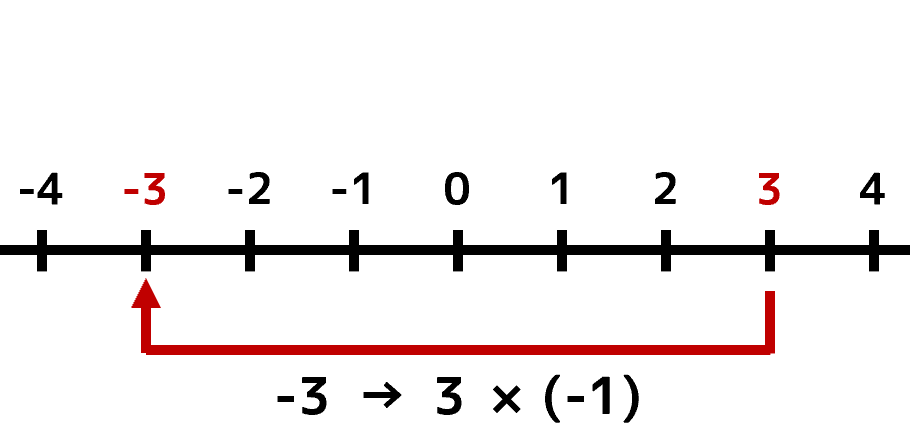
もちろん、この考え方は「負の整数にマイナス(-)をつけた」場合も同様です。「-3」にマイナス(-)をつけた「-(-3)」は「3」です。
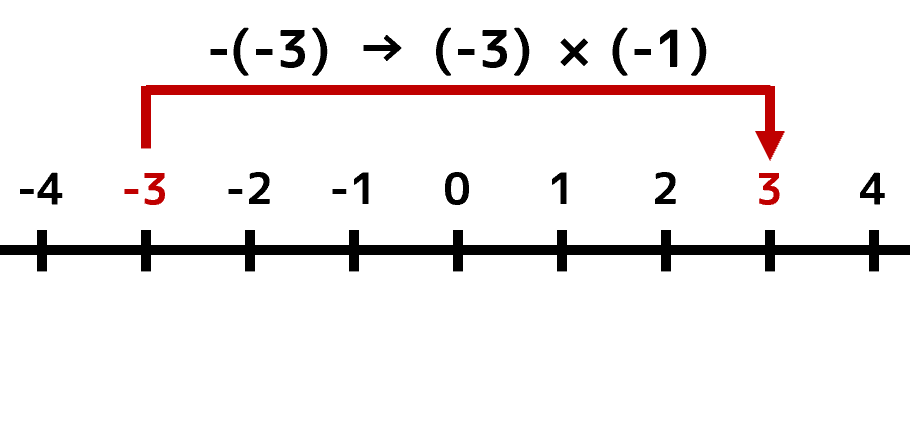
では「3」にマイナス(-)を2つつけたら、どうなるでしょう。つまり「--3」です。これは「-1を掛け算する」を2回行うのですから、元の「3」に戻ってきます。
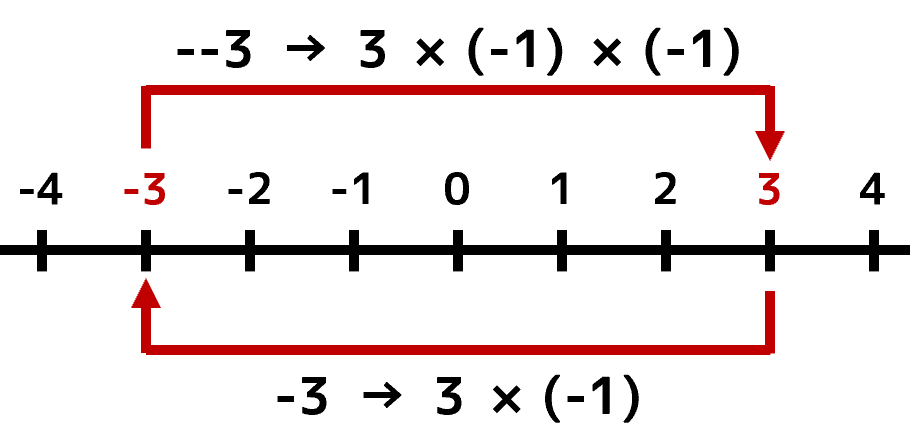
整数にマイナス(-)を2つつけると、元の整数に戻ります。つまり「--」というのは「計算しても結果を変えない」計算をしたことになります。最後に、この計算を"TRUE"と"FALSE"の論理値でみてみましょう。
| 論理値 | 計算での値 | - ×(-1) |
-- ×(-1)×(-1) |
|---|---|---|---|
| TRUE | 1 | -1 | 1 |
| FALSE | 0 | 0 | 0 |
何のために?
「--」は、"TRUE"と"FALSE"を「1」と「0」に変換するための「計算しても結果を変えない」計算です。でも、それだったら別に「1を掛け算」したって「0を足し算」しても、同じことです。

だったらなぜ「*1」ではなく「--」を使った数式を、たびたび見かけるのでしょうか。ここからは私の推測ですが、おそらく「何かよくわかんないけど、何となくカッコイイから」でしょう。インターネットの掲示板などでは、マウントの取り合いです。そこでは、誰もが容易に分かる簡単な方法よりも、見た者を驚かせるような知られていない方法が評価されます。「*1」や「+0」の意味は、小学生でも分かります。しかし「--」という書き方に馴染み深い人は、おそらくそれほど多くないと思います。ましてマイナス記号(-)は、一般的に「5-3」などの引き算で使われることが多く、今回のように正負を反転させる目的で使われるのはレアケースです。しかも、今回はその記号を「--」と2回続けているのですから、初見の人に与えるインパクトも大きいでしょう。余談ですが、「5-3」など引き算で使われるマイナス記号を二項演算子と呼び、「-3」のように正負を反転させるマイナス記号のことを単項演算子と呼びます。
今回は、「--」の使用例として、"TRUE"や"FALSE"を「1」や「0」に変換するケースをご紹介しましたが、「計算しても結果を変えない」計算を行う機会はほかにもあります。たとえば、文字列形式の「"1"」を数値の「1」に変換するような場合です。
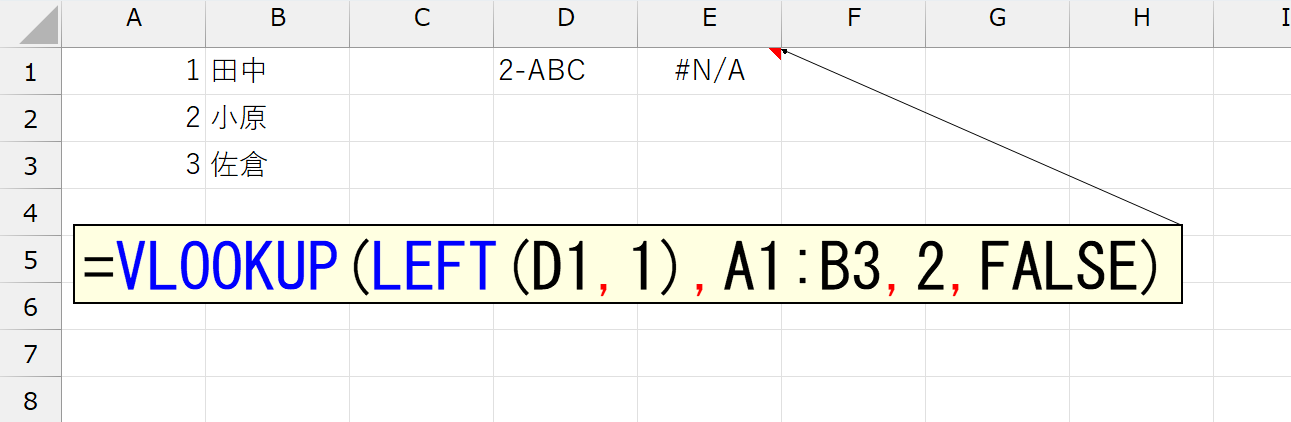
上図は、VLOOKUP関数でA列を探し、見つかったB列を返す数式です。探すのは、セルD1に入力されている文字列の「左1文字」です。LEFT関数で抜き出しています。さて、「2」に該当する"小原"が返ると思いきや、数式はエラーになりました。理由は、A列に入力されている「1」「2」「3」が数値なのに対して、LEFT関数の結果は"2"という文字列だからです。VLOOKUP関数は、このへんの融通が利きません。解決策は、LEFT関数の結果を「数値に変換」してやります。そう、ここでも「計算しても結果を変えない」計算を行います。

解説は以上です。使うのなら、意味と動作を理解し、代替案と比較して、「--」にメリットがあると判断したときに使ってください。ちなみに私は実務で使ったことは一度もありません。メリットがあるとは思えないからです。くれぐれも「よく分かんないけど」「なんか上級者っぽいし」「裏技みたいだから」という、理由にならない理由で採用しないよう、お気をつけくださいな。